期权风险敏感因子简介与应用

　　豆粕和白糖期权即将上市，商品期权作为新的金融衍生工具，将为商品投资者提供更多的投资和避险功能。我们知道，不同于期货的线性损益特征，期权的损益状况为曲线，买方和卖方权利义务不对等。

　　此外，期权价格受标的价格S、执行价格X、期限T、无风险利率r、波动率σ等因素的影响，那么如何衡量它们的变化对期权价格的影响呢？一般用希腊字母Greeks——Delta、Gamma、Vega、Theta、Rho来表示这些变化关系。

　　期权价格曲线

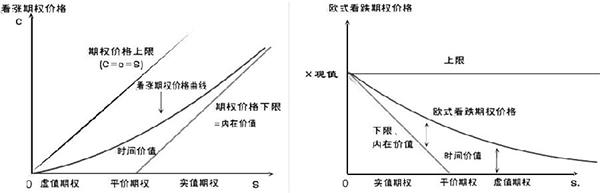　　　　我们平常看到的期权折线图是期权到期日的价格，仅包含内在价值，但在实际交易过程中，期权价格绝大多数时间为未到期日价格，表现为曲线形式，包含内在价值和时间价值两部分。

　　时间价值源于期权多头权利义务不对称这一特性，在期权尚未到期时，标的资产价格的波动为期权持有者带来收益的可能性或隐含价值。因此，期权价格的时间价值有时也称为波动价值。

　　期权敏感因子简介

　　Delta值

　　Delta值是期权价值对标的资产价格的偏导数，即期权价格曲线的斜率，用来衡量标的价格变动带来的期权价格变动风险。其中，看涨期权的Delta值是正值，介于0—1之间；看跌期权的Delta值是负值，介于-1—0之间；平值期权的Delta值约等于±0.5。需要指出的是，风险指标的正负号是从买入期权的角度来考虑的，在实际交易过程中，需要注意期权指标与部位指标的区别。

　　Delta值主要有以下特征：一是Delta值可以相加；二是Delta值为零的头寸被称为Delta值中性；三是由于标的资产价格引起Delta值变动，Delta值中性是动态的概念。

　　例如，假设在期权投资组合内，头寸一的Delta值为0.5，头寸二的Delta值为-0.4，则组合的总Delta值为0.5-0.4=0.1，相当于持有0.1手期货多头头寸。

　　Gamma值

　　Gamma值是期权价值对标的资产价格的二阶偏导数，也是期权Delta值对标的资产价格的偏导数，即Delta值曲线的斜率，用来衡量期权价格变动带来的Delta值变动风险。

　　期权买权的Gamma值为正，期权卖权的Gamma值为负，即买入看涨期权、买入看跌期权的Gamma值为正值，卖出看涨期权、卖出看跌期权的Gamma值为负值。

　　Gamma值主要有以下特征：一是只有期权有Gamma值；二是证券组合Gamma值为零时，称为处于Gamma值中性状态；三是Gamma值中性是为了消除Delta值中性的误差，同样也是动态的概念。

　　Vega值

　　Vega值是期权价值对标的资产波动率的偏导数，度量期权价值对标的资产波动率的敏感性。其中，期权买方的Vega值为正值，期权卖方的Vega值为负值；不同内涵价值的期权合约Vega值也不相同，平值期权的Vega值大于实值期权或者虚值期权。

　　Theta值

　　Theta值的大小反映了期权购买者随时间推移所损失的价值，用来衡量期权理论价值随着到期日的临近而下降的速度，是时间变化的风险度量指标。无论是看涨期权还是看跌期权，随着到期日的临近，期权理论价值都会加速下降。

　　一方面，期权买方的Theta值为负值，即到期期限减少，期权价值相应减少，期权卖方的Theta值为正值；另一方面，不同内涵价值的期权合约Theta值也不相同，平值期权的Theta值大于实值期权或者虚值期权。

　　Rho值

　　Rho值是期权价格的变化与利率变化之间的比率，衡量期权理论价值对利率变动的敏感性。

　　期权敏感因子应用

　　Delta值对冲

　　实际操作过程中，在考虑最终行权的情况下，只需要保证期权对应的标的头寸与投资者需要套保的头寸相等即可。如果仅考虑期权、期货等头寸在价格上的对冲，则需要保持Delta值中性。

　　需要注意的是，期权Delta值非线性。在进行Delta值中性对冲操作的过程中，Delta值会因期权价格的变化而发生改变，导致Delta值中性失效。因而需要在Delta值中性策略中进行动态调整，不断保持投资组合的Delta值为零。

　　Gamma值对冲

　　由于保持Gamma值中性只能通过期权头寸的调整获得，实现Gamma值中性的结果往往是Delta值非中性。因而常常还需要运用标的资产或期货头寸进行调整，才能使得证券组合同时实现Delta值中性和Gamma值中性。由于期权Gamma值非线性，同样是动态的概念。

　　综合分析，期权最大的特点就是非线性，期权价格非线性，期权敏感因子也非线性。因此，在实际操作中，Delta值中性对冲和Gamma值中性对冲都是动态的概念，需要不断调整头寸以保持中性状态。